DEFINICION DE DERIVADA

¨PENDIENTE DE LA tan A UNA CUERVA EN UN PUNTO DETERMINADO¨



REGLAS DE DERIVADAS DE FUNCIONES ALGEBRAICAS

-       La derivada de una constante es igual a 0

Si y=c

y’=0

-       La derivada de una variable independiente es igual a uno.

Si y=x

y’=1

-       La derivada del producto de una constante por una variable independiente es igual a la misma constante

Si y=cx

y’=c

-       La derivada de x^n es igual al producto del exponente n por x con exponente disminuido en una unidad

Si y= x^n

y’= nx^n-1

 El producto del exponente n por su exponente disminuido en una unidad por el producto de la derivada del termino u

Si y= u^n

y’= nu^n-1 d/dx U

-        La derivada de Raiz de n es un cociente cuyo numerador es la derivada de u y el denominador es dos veces la misma raíz.

Si y= √n

y’= d/dx n / 2√u

-        La derivada de la suma de un numero finito de funciones es igual a la suma de las derivadas de las funciones

Si y= u + v + w

y’= d/dx(u) + d/dx(v) + d/dx (w)

-        La derivada del producto de las dos funciones es igual al producto de la primera función por la derivada de la segunda mas el producto de la segunda por la derivada de la primera

Si y= u.v

y’= u d/dx (v) + (v) d/dx u

-        La derivada del cociente de dos funciones es igual al denominador por la derivada del numerador menos el numerador por la derivada del denominado, todo dividido por el cuadrado del denominador

Si y= u / v

y’= v d/dx (u) – (u) d/dx v  / v^2

REGLAS DE DERIVADAS DE FUNCIONES TRASCENDENTES- TIGONOMETRICAS, EXPONENCIALES, LOGARITMICAS DE BASE Y NATURALES.

-       La derivada de seno.

Si y= senu

y’= cosu d/dx (u)

-       La derivada de coseno.

Si y= cosu

y’= -senu d/dx (u)

-       La derivada de tangente.

Si y= tanu

y’= sec^2u d/dx (u)

-       La derivada de Cotangente.

Si y= cotu

y’= -csc^2u d/dx (u)

-       La derivada de Secante.

Si y= secu

y’= secu.tanu d/dx (u)

          La derivada de cosecante.

Si y= cscu

y’= -cscu.cotu d/dx (u)

-       La derivada de a^u.

Si y= a^u

y’= a^ulna d/dx (u)

-       La derivada de e^u.

Si y= e^u

y’= e^u d/dx (u)

-       La derivada de Logaritmo Natural .

y= lnu

y’= 1/u d/dx (u)

-       La derivada de logaritmo base.

y= logaU

y’=1/Ulna d/dx (u)

*PASOS DE RESOLUCION, USOS Y APLICACIONES (DERIVACION).

1 er PASO. Sumar el Incremento Delta (∆) representado por un triangulo a cada variable.

2do PASO. Desarrollar operaciones algebraicas y restarle la función original.

3er PASO. Dividir entre el incremento de ∆x. Para eliminar valores delta (∆x)

4to PASO. Aplicar el limite ∆x cuando tiende a 0. Sustituiremos todos los ∆x por [0] en toda la ecuación y se multiplicara.

Usos y Aplicaciones:

La derivada se desarrollo con el deseo de medir y cuantificar el cambio y variacion.

Newton y Leibnitz fueron independientemente los introductores de este estudio deoperaciones.

Cuando se tiene la gráfica de una función continua resulta bastante fácil señalar en qué intervalo la función es creciente, decreciente o constante. Sin embargo, no resulta fácil decir en que intervalo la función es creciente, decreciente o constante sin la gráfica de la función.

El uso de la derivada de una función puede ayudar a determinar si una función es creciente, decreciente o constante en un intervalo dado. 

* MAXIMOS Y MINIMOS

Los maximos y minimos de una funcion de dos variables nos permiten medir las altitudes maximas y minimas sobre la superficie que integra la grafica de la funcion (Son parecidas al punto mas alto de una colina y el mas bajo de una hondeada).

*ABSOLUTOS Y RELATIVOS

Maximo Absoluto
Una función tiene su máximo absoluto en el x = a si la ordenada es mayor o igual que en cualquier otro punto del dominio de la función.

Mínimo absoluto
Una función tiene su mínimo absoluto en el x = b si la ordenada es menor o igual que en cualquier otro punto del dominio de la función.

Maximo y Minimo Relativo
Una función f tiene un máximo relativo en el punto a, si f(a) es mayor o igual que los puntos próximos al punto a.
Una función f tiene un mínimo relativo en el punto b, si f(b) es menor o igual que los puntos próximos al punto b.

*PUNTO DE INFLEXION

Es un punto donde los valores de x de una funcion continuapasa de un tipo concavidad a otra. La curva atraviesa la tangente. La derivada de la segunda funcion f en el puntode inflexion es cero, o no existe. 

* VALORES CRITICOS

En cálculo, los valores críticos de una función de una variable real es cualquier valor en el dominio en donde la función no es diferenciable o cuando su derivada es 0.

Por el teorema de Fermat, los máximos y mínimos locales de una función pueden ocurrir únicamente en sus puntos críticos. Sin embargo, no todo punto estacionario es un máximo o mínimo de la función; puede corresponder también a un punto de inflexión de la gráfica, como para ƒ(x) = x3 en x = 0, o la gráfica puede oscilar en la vecindad del punto, como en el caso de la función definida por la fórmula ƒ(x) = x2sen(1/x) para x ≠ 0 y ƒ(0) = 0, en el punto x = 0.

*SENTIDO DE CONCAVIDAD

f presenta concavidad positiva en x=a si existe un E*a / para todo x perteneciente al E*a f(x) > f'(a)(x-a) + f(a).
 

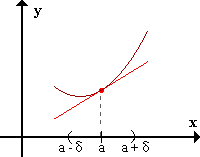
La función presenta concavidad positiva en el punto a si, en un entorno reducido de a, la gráfica de f está "por encima" de la recta tangente a f(x) en el punto a.


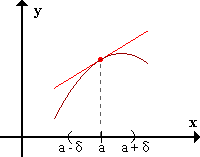
f presenta concavidad negativa en x=a si existe un E*a / para todo x perteneciente al E*a f(x) < f'(a)(x-a) + f(a).
 

La función presenta concavidad negativa en el punto a si, en un entorno reducido de a, la gráfica de f está "por debajo" de la recta tangente a f(x) en el punto a.

*Segunda derivada

Se llama derivada segunda de una función f(x) a la derivada de la derivada de dicha función.
Notación: f''(x).
Este concepto se puede extender a la derivada n-ésima de una función.