DEFINICION DE LIMITES

El vocablo que nos ocupa en primer lugar, límite, podemos decir que se trata de una palabra, que puede traducirse como “frontera o borde”.

 Puede tratarse de una línea que separa dos territorios, de un extremo a que llega un determinado tiempo o de una restricción o limitación.

La expresión límite de una función se utiliza en el cálculo diferencial matemático y refiere a la cercanía entre un valor y un punto. Por ejemplo: si una función f tiene un límite X en un punto t, quiere decir que el valor de f puede ser todo lo cercano a X que se desee, con puntos suficientemente cercanos a t, pero distintos.

TIPOS DE LIMITES

LIMITES FINITOS

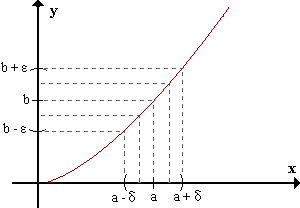
Limf(x)=b <=> para todo ε>0 existe δ>0 / para todo x, 0 < |x-a| < δ |f(x) - b| < ε.

x->a


Se dice que la función f(x) tiene límite b, cuando x tiende a a, si dado ε positivo arbitrario y tan pequeño como se quiera, existe un δ tal que para todo x perteneciente al entorno reducido de a de radio δ, la función pertenece al entorno de b de radio ε.

.

LIMITES INFINITOS

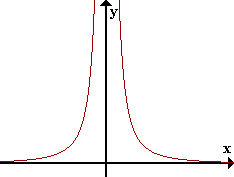
Observemos la función f(x)=1/x2 para valores de x positivos muy grandes.

x f(x)

100 1,0x10-4

1.000 1,0x10-6

10.000 1,0x10-8

100.000 1,0x10-10

1.000.000 1,0x10-12

Si tomamos x cada vez mayor, f(x) está cada vez más cerca de 0. Si x es suficientemente grande podemos conseguir que f(x) se acerque a 0 tanto como queramos. Decimos que f(x) tiende a 0 cuando x tiende a infinito.

Ilustración geométrica del límite infinito

Veamos a continuación las definiciones precisas de cada uno de los límites que involucran al infinito.

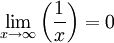
CONDICIONES DE CONTINUIDAD 

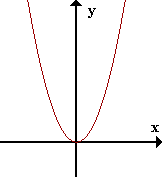
Intuitivamente, la continuidad significa que un pequeño cambio en la variable x implica sólo un pequeño cambio en el valor de f(x), es decir, la gráfica consiste de un sólo trozo de curva.



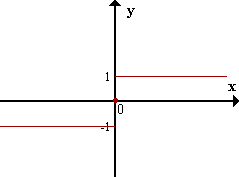
En contraste, una gráfica como la de la función f(x) = sgn x (signo de x) que consiste de pedazos de curva separados por un vacío en una abcisa exhibe allí una discontinuidad.

La continuidad de la función f(x) para un valor a significa que f(x) difiere arbitrariamente poco del valor f(a) cuando x está suficientemente cerca de a.